The human brain, performs computations of incredible complexity with astonishing energy efficiency – a mere ~20 watts (see Boahen 2022 ). Our current advances in AI based on deep learning of artificial neuronal networks directly stem from inspiration of biological neuronal networks. However, even the most powerful AI guzzle megawatts while still struggling to match the brain’s flexibility and learning capabilities.
Why is this important? 1) increasing reliance on fossil fuels to feed AI is certainly the wrong direction and 2) current AI performance is plateauing and simply scaling up is not overcoming the limitation.
What if we are missing other insights from biological networks. And there are many insights, eg. spatiotemporal patterns, inhibition… But let’s first look at dendrites and compartmentalisation, as I recently published about it (Kelly et al BioRxiv 2025). While we’ve long viewed the neuron as the fundamental computational unit, emerging research, suggests a far more nuanced and powerful reality: the intricate architecture of dendrites, particularly their compartmentalisation, is a key to unlocking the brain’s extraordinary computational prowess.
What is a Computational Unit? Beyond the Point Neuron
The Computer Science Perspective
In computer science, a computational unit is typically defined as the smallest entity capable of performing an operation or processing information. Think of a transistor in a CPU, a logic gate, or a single processing core. These units take inputs, apply a set of rules or functions, and produce an output. The power of a computer often scales with the number of these units and how efficiently they can communicate and operate in parallel.
The Traditional Neuroscience View: The Neuron as a Computational Unit
For decades, neuroscience has largely conceptualized the neuron as the primary computational unit. This ‘point neuron’ model simplifies the neuron to a single input-output device: it receives signals from other neurons at its synapses, sums these inputs, and if a certain threshold is reached, fires an action potential (output). This model has been incredibly useful for understanding basic neural circuits and forms the basis of most artificial neural networks (ANNs).
Figure 1: Point Neuron as a transistor: A simple diagram showing a basic logic gate (e.g., AND gate) with inputs (a, b) when both active output (c), illustrating the fundamental concept of a computational unit in computer science. The point neuron receives inputs that are integrated non-linearly to produce an output.
The Dendrite as a Micro-Processor
However, this traditional view is no longer accepted in neuroscience. Dendrites are the tree-like extensions that receive synaptic inputs but they are far more than just input antennae; they are sophisticated information processors in their own right. A wealth of research now shows that dendrites are not merely passive cables funnelling information to the cell body. Instead, they are highly active, dynamic structures capable of complex, localized computations.
Information Processing at the Branch Level
Each dendritic branch, and even sub-regions within a branch, can independently process incoming synaptic signals. This allows a single neuron to effectively perform multiple, parallel computations in each branch simultaneously.
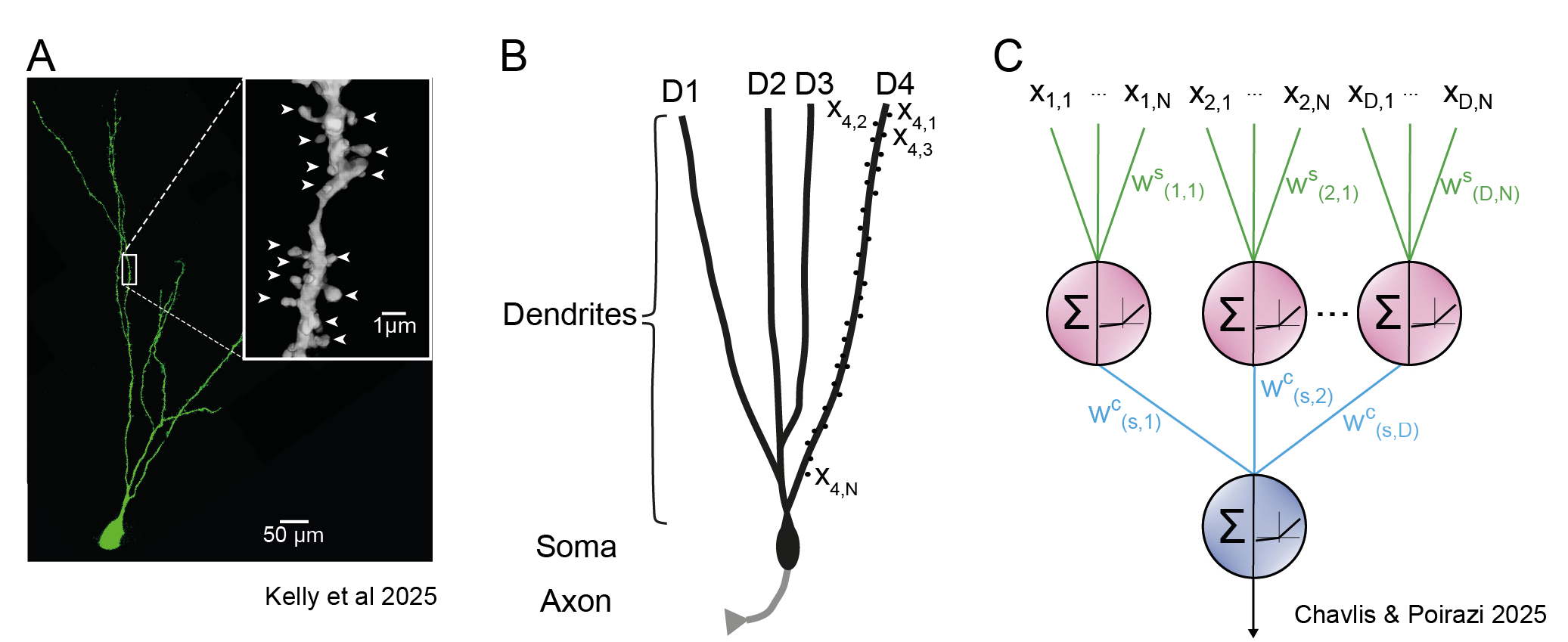
Figure 2: Dendrites as a computational unit. A, Picture of neuron showing soma and dendrites with the highlighted segment of dendrite at high resolution in inset. Each dendrite is studded with spines (see arrows inset) which are individual inputs onto the dendrite. Each neuron has 10s of thousands of these spines. Adapted from Kelly et al BioRxiv 2025. B, Schematic representation of a neuron with 4 dendritic branches connected to a soma and axon as output. C, Computational representation of a neuron with dendrites as another computational layer. Each input Node denoted on each dendrite as (xD,N) integrated non-linearly with a synaptic weight (WS(D,N)) in each dendritic branch. In turn, output of each dendrite is integrated non-linearly at the soma with dendritic compartment weight (WC(S,D)). Adapted from Chavlis & Poirazi 2025 Nat. Comms.
Some key points about dendritic computations, in each branch they are often highly non-linear. Unlike a simple sum, the response of a dendritic segment to multiple inputs isn’t just additive. The timing, location, and strength of inputs, combined with the active properties of the dendritic membrane (like voltage-gated ion channels), can lead to complex interactions and supra-linear (or sub-linear) responses. This non-linearity is critical for performing sophisticated computations.
Perhaps most strikingly, individual dendrites have been shown to perform complex logic operations, including the notoriously difficult XOR (exclusive OR) operation. In computer science, XOR requires two inputs to be different to produce a “true” output. While a single point neuron cannot perform XOR, a single neuron with appropriately structured dendrites can. This highlights the immense computational power hidden within these seemingly simple structures.
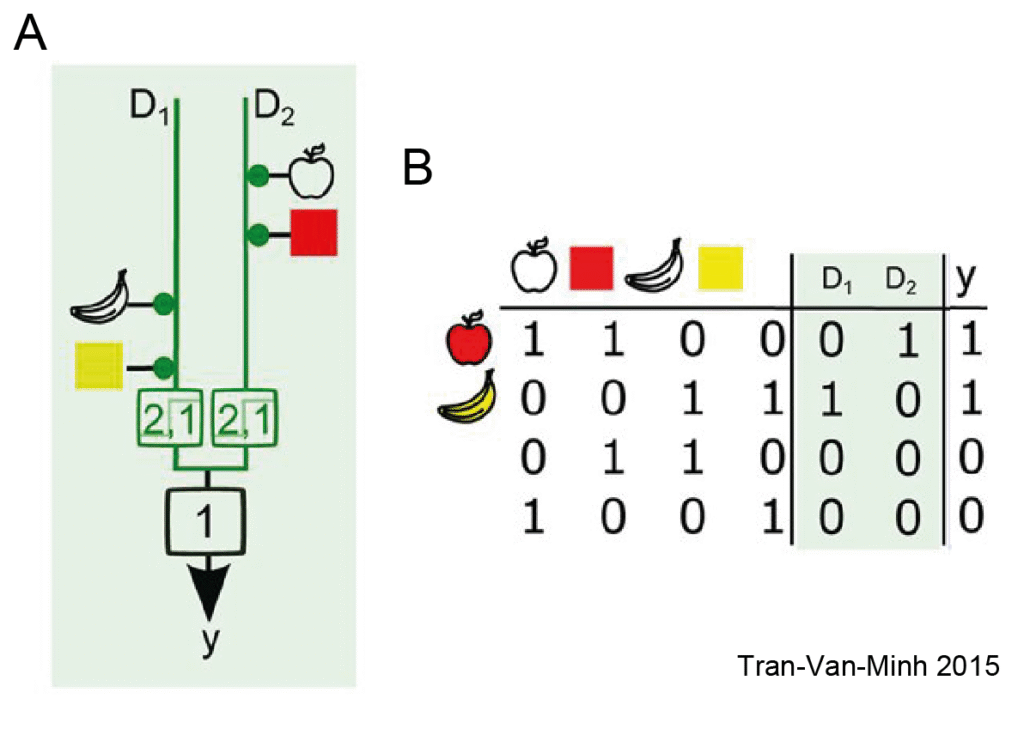
Figure 3: Dendrites capable of exclusive or computation. A Schematic illustrating the structure of colour and shape input onto a dendritic branch. B Truth table showing only correct colour and shape combination activated respective dendrite and neuron output. The non-existent red banana will not.
The Power of Compartmentalization: Dividing and Conquering Information
So, if dendritic branches compartmentalise computations what does that mean for information processing in the neuron. Firstly, dendritic compartmentalization refers to the anatomical and physiological division of dendrites into distinct functional units. The complex morphology with various degrees of branching and active ion channels distributed unevenly along their length creates electrotonic compartments – regions where electrical signals are relatively isolated from other parts of the dendrite.
This compartmentalization serves several crucial functions:
- Increased Computational Capacity: By allowing different parts of a dendrite to perform independent computations, compartmentalization vastly increases the effective computational power of a single neuron
- Enhanced Specificity and Learning: Localized computations allow the neuron to respond to highly specific patterns of synaptic input. This specificity is crucial for learning and memory formation. Changes in synaptic strength (plasticity) can occur locally within a compartment without broadly affecting the entire neuron’s processing.
- Energy Efficiency: Performing computations locally reduces the need for signals to travel long distances to the soma, thereby reducing the energy expenditure associated with propagating action potentials. This contributes significantly to the brain’s remarkable energy efficiency.
Combining these features converts a single pyramidal neuron into a deep layer network. Above I showed the neuron with dendrites as 2 layers but others have shown an individual neuron is more realistically the equivalent to at least a 5-layer network, vastly increasing the computational power of a point neuron (Beniaguev et al 2021).
Dendrites and the Future of Artificial Neural Networks
Current Artificial Neural Networks (ANNs), the backbone of modern AI, are predominantly built upon the ‘point neuron’ model which is fully connected and learning is achieved by adjusting the weight of each input of each point neuron in each layer in a process know as backpropagation. While highly successful in many applications, this approach has inherent limitations and efficiency challenges. Adjusting the enormous number of trainable synaptic weights is costly, computational and energetically. Kwabena Boahen’s work at Stanford, highlighted the inefficiency of this ‘synaptocentric’ view and proposed ‘dendrocentric’ neuromorphic chip architecture in his Nature paper “Dendrocentric learning for synthetic intelligence“.
But rather than change chip design what about changing ANN architecture? Would this improve efficiency. The latest work from Spyridon Chavlis and Panayiota Poirazi builds on the idea of integrating dendritic processing into ANNs (Chavlis & Poirazi 2025). The work demonstrates that models incorporating active dendrites can achieve comparable or even superior performance to traditional ANNs with far fewer parameters and reduced computational costs. A big factor in this is how the input is structured and that is not always clear. Nevertheless, this is a direct validation of the idea that dendritic complexity is a powerful asset.
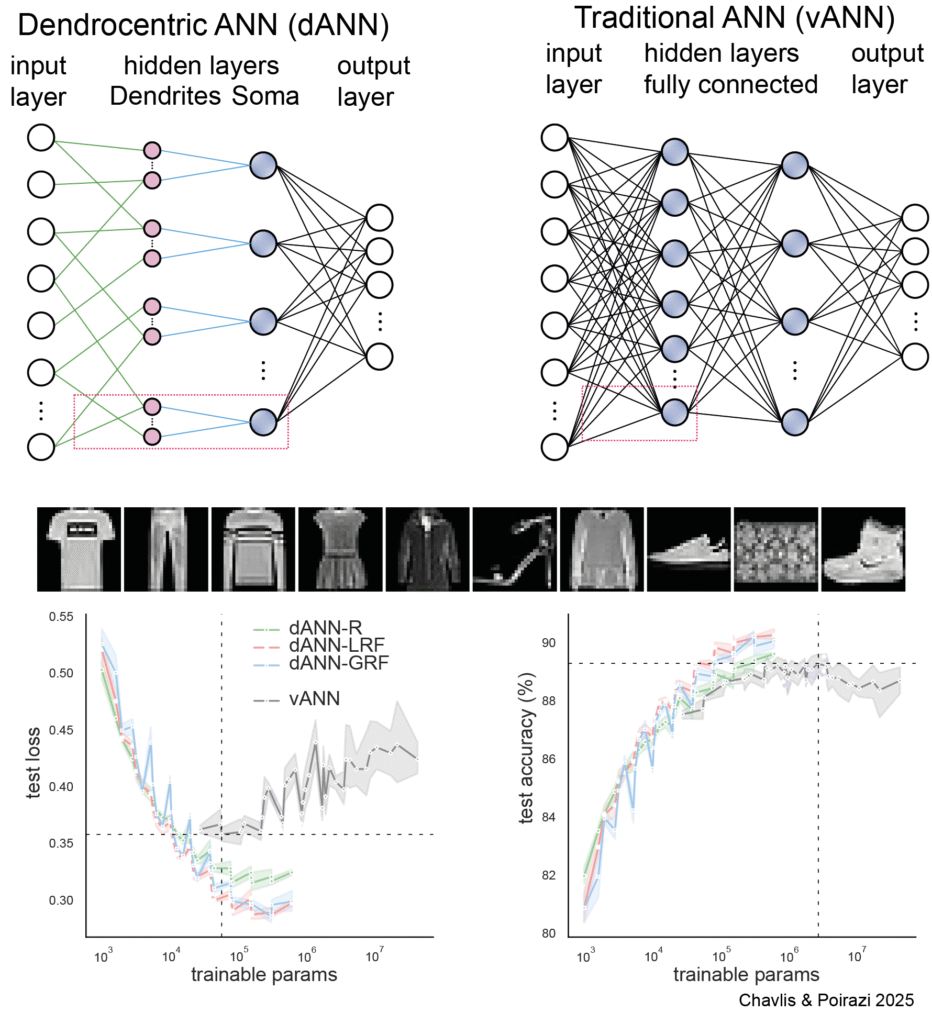
Figure 4: Dendritic ANN improves accuracy and reduces trainable parameters. Dendritic neuron architecture with a somatic node (blue) connected to several dendritic nodes (pink). Dendrites are connected solely to a single soma, creating a sparsely connected network. Traditional fully connected ANN with two hidden layers. Nodes are point neurons (blue) consisting only of a soma. The Fashion MNIST dataset was used and models tested on ability to categorise items. Dashed lines denote optimum of the vanilla ANN. Different input structure to the dANN was tested with random input structure on the dendrite (dANN-R), local receptive fields (-LRF) or global receptive fields (-GRF). All dANN input structures performed better with fewer trainable parameters compared with the vANN. Also notice the dANNs were less prone to overfitting and the increase in loss with increasing trainable parameters seen in vANN.
Conclusion: The Future is Branched
The journey to energy-efficient AI cannot lie in simply scaling ANNs, building bigger models with more simplified neurons. But understanding and the brain’s nuanced computational strategies may provide insights. The emerging understanding of dendrites as dynamic, compartmentalized computational units offers a altermative paradigm. By embracing this complexity, both in our theoretical models and in the design of next-generation AI, we stand to create systems that are not only more powerful but also more efficient, bringing us closer to unlocking the full potential of artificial intelligence, inspired by the brain’s branched and beautiful computational units.
Leave a Reply